Data Structure and Algorithms - 2024년12월08일

• tag : Computer_Science |

Introduction to Data Structures

Data Structures

데이터를 구성, 저장, 조작하는 방법을 의미함 [ 데이터의 관리 효율성을 조절하기 위한 여러가지 구조에 관한 내용 ]
대표적으로 Array, List, Stack, Queue, Tree, Graph 가 있다.

Abstract Data Type(=ADT)

프로그래밍을 함에 있어 데이터를 추상화하여 논리적인 구조를 정의한 것

• 장점
  1. 데이터에 대한 정보를 이해하고 저장하는 방식을 결정함으로써 최적의 알고리즘을 개발할 수 있음
  2. 프로그래밍을 효율적으로 구현할 수 있도록 도와줌
• Abstract

  복잡한 데이터나 시스템 등으로부터 핵심적인 개념 또는 기능을 간추려 내는 것
  실제 데이터의 형태를 그대로 다루는 것이 아니라 데이터가 가져야하는 명세(specification)를 기반으로 만듬

Time and space complexity

• Time complexity : 프로그램이 실행되고, 완료되는데 걸리는 시간

  Compile Time
  Execution Time [ 주로 이 복잡도 사용 ]

• Space complexity : 프로그램이 실행되고, 완료되는데 필요한 메모리

  고정 공간 요구량 : 자료구조가 사용하는 고정된 메모리 공간을 의미[Ex. int, double]
  가변 공간 요구량 : 필요에 따라 동적으로 할당, 해제되는 메모리 공간을 의미[Ex. function call]

• Big Oh, Big Ω, and Big Θ notation

  Big oh : 최악의 경우
  Big Ω : 최선의 경우
  Big Θ : 평균

Stacks and Queues

Stack

LIFO(Last-In, First-Out) 구조를 가진 자료구조
가장 최근에 삽입한 요소를 top이라고 지칭한다.
Stack의 구조는 컴퓨터 가상메모리의 Stack 영역에서 사용되는데, 함수가 호출되면서 다시 복귀할 주소를 저장하거나, 지역변수, 매개변수 등을 임시로 저장하는데에 쓰인다.

Queues

FIFO(First-In, First-Out) 구조를 가진 자료구조
front와 rear로 가장 먼저 들어온 요소와 제일 마지막에 들어온 요소에 접근한다.
Enqueue : queue에 원소를 삽입 | Dequeue : queue에서 원소를 삭제

Linked List and Hash Table

Array

연속된 메모리 공간에 같은 타입의 데이터를 순차적으로 저장하는 자료구조
크기가 고정되어 있기 때문에 배열을 생성할 때 크기를 지정해줘야함[ 배열이 가득 차는 경우 새로운 데이터를 추가할 수 없거나 기존 데이터를 삭제해야 함 ]

Linked List

생성 후에 자유롭게 원소를 추가/삭제할 수 있는 자료구조
가변적인 길이를 가지고 있기 때문에, 새로운 데이터 추가에 대한 제한이 거의 없다는 장점이 있다.

Hash Table

데이터의 key를 hash function 을 통해 hash value으로 변환하고, 이 값을 인덱스로 사용하여 데이터를 저장하거나 검색하는 효율적인 자료 구조
평균적으로 O(1)의 시간 복잡도로 데이터에 접근할 수 있다.
Hash Table의 사용 목적은 정해진 메모리에 여러 원소를 효율적으로 저장하여 indexing 성능을 O(1)에 가깝게 만드는 것
Hash function을 통해 hashing을 하게 되면 다른 원소가 같은 index를 가지는 hash collision이 발생

• Hash Collision을 해결하기 위한 방법
  1. Separate Chaining

     방법 : 해시 테이블의 각 인덱스에 연결 리스트나 다른 자료 구조를 사용하여 여러 개의 key-value pair를 저장
     장점 : 간단하고 동적으로 크기를 조절하기 쉽다.

  2. Open Addressing

     방법 : 충돌이 발생하면 다른 빈 슬롯을 찾아 데이터를 저장

Trees and Graphs

Tree는 데이터 속 항목을 계층적으로 구조화하는 자료구조

• 용어
  1. Node : 트리 구조의 교점으로 Node는 데이터(value)를 가지고 있고, 자식노드를 가지고 있다.
  2. Root Node : 트리 구조에서 가장 위에 있는 노드, 즉 시작점이 되는 노드
  3. edge(link) : 트리를 구성하기 위해 노드와 노드를 연결하는 선
  4. level : 트리의 특정 깊이를 가지는 노드의 집합
  5. degree : 각 노드가 지닌 가지의 수를 말하며 ‘차수’라고도 함
  6. Leaf Node(Terminal Node) : 하위에 다른 노드가 연결되어 있지 않은 노드
  7. Internal Node : Leaf노드를 제외한 중간에 위치한 노드들
  8. Depth(=Height) : 트리에 가장 큰 Level의 숫자

Type of Trees

Binary Tree

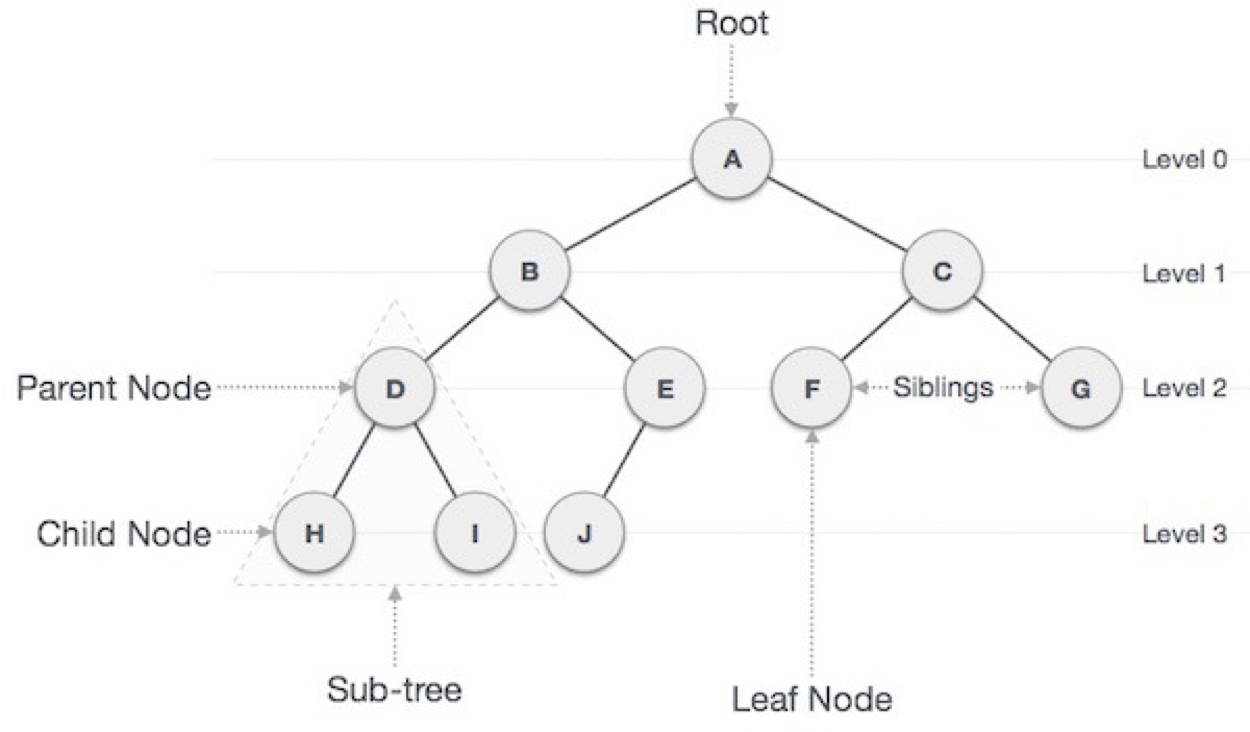
자식 Node가 최대 둘 뿐인 Tree
Decision Tree중에 가장 많이 사용되는 CART(Classification and Regression Tree)가 있다.

Balanced Tree

어느 한쪽으로 데이터가 치우치지 않도록 균형을 지킬 수 있는 규칙을 가지고 있다.
검색용 tree들은 다 검색 효율성을 위해 balanced tree로 정의[Ex. B-tree, B+ tree]

Graphs

그래프는 관계를 모델링 하기 위한 자료구조

• 용어
  1. Vertex(=Node) : Tree에서 Node와 같은 개념
  2. Edge(=link) : 정점과 정점을 있는 선
  3. weight : edge의 가중치 값
  4. degree : Vertex에 연결되어 있는 Edge 수

     out-degree : 방향이 있는 그래프에서 정점에서부터 출발하는 간선의 수 in-degree : 방향이 있는 그래프에서 정점으로부터 들어오는 간선의 수

  5. Path : \(V_i\)에서 \(V_j\)까지 간선으로 연결된 정점을 순서대로 나열한 리스트

     Ex. A -> E : {A, B, D, E}

  6. Path length : 경로를 구성하는 간선의 수
  7. Cycle : 경로 중에서 경로의 시작 정점과 마지막 정점이 같은 경로

Undirected Graph

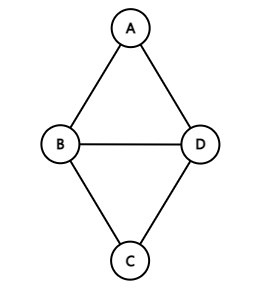
두 정점을 연결하는 간선에 방향이 없는 그래프, 가장 기본적 [ (A, B) == (B, A) ]

Directed Graph

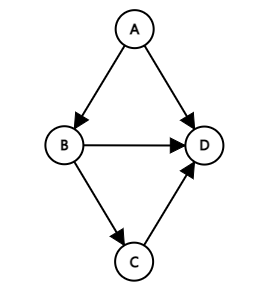
간선에 방향이 있어 정해진 방향으로만 이동할 수 있는 그래프 [ <A, B> : A는 출발 정점, B는 도착 정점 ]

Weighted Graph

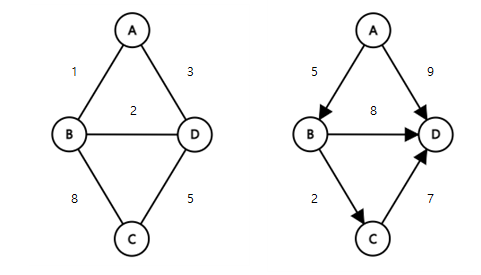
정점을 연결하는 간선에 가중치(Weight)를 할당한 그래프

Basic Algorithm Design

• Algorithm은 어떠한 문제를 해결하기 위해 정해진 일련의 절차나 방법을 공식화한 형태로 표현한 것
• Algorithm은 입력, 출력, 명확성, 유한성, 효율성의 조건을 만족해야 한다.
• 좋은 Algorithm이란 효율성을 고려한 Algorithm -> 공간복잡도와 시간복잡도를 고려해 알고리즘을 짜야함[‘efficiency’]

Sorting Algorithm

주어진 데이터를 정해진 순서대로 재배열하는 알고리즘이다.

-> 데이터 간의 비교가 가능해야 함
-> 비교를 하려면 기준이 있어야 함
-> 기준을 정하려면 계산 방법이 있어야 함

Bubble Sort

• Time complexity : \(O(N^2)\)
• 인접한 두 원소를 비교하면서 큰 값을 뒤로 보내며 정렬이 이루어짐

Selection Sort

• Time complexity : \(O(N^2)\)
• 리스트에서 최솟값을 찾아 맨 앞의 요소와 위치를 바꾼다.

Insertion Sorting

• 리스트의 요소를 하나씩 가져와서 이미 정렬된 앞 부분과 비교하여 적절한 위치에 삽입함.

Quick Sort

• 분할 정복(divide and conquer)방법을 통해 리스트를 정렬하는 알고리즘

  분할 정복이란? 복잡한 전체의 문제를 부분으로 나누어, 부분적인 문제를 해결하고 다시 합쳐 전체를 해결하는 방식

• 구현 방식

Searching Algorithm

Linear Search(순차 탐색)

• Time complexity : \(O(N)\)
• 처음부터 끝까지 순서대로 모든 데이터를 탐색하는 방법

Binary Search(이진 탐색)

• 정렬된 데이터에서 특정 값을 찾을 때 사용하는 방법[Time complexity : \(O(log_{2}N)\)]
• IF 정렬이 안되어있을 때, 정렬하는데 O(NlogN)시간을 지불하고 사용 가능!

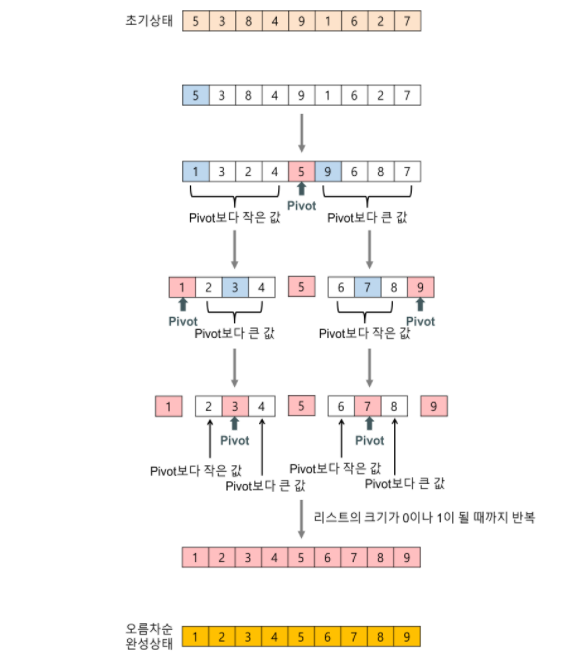
정렬이 되어있지 않을 때
- Linear Search : m * O(N)
- Binary Search : O(NlogN) + m * O(logN)
> m < logN 이면, Linear Search를 사용, 그렇지 않으면 Binary Search를 사용