

그 자료는 반드시 특정한 가정들을 만족하는 모수적 자료
** 모수적 검정의 네 가지 기본 가정
정규성을 점검하는 것이 유익하다. [ 단순히 표본이 크거나 표본 자료가 정규분포를 따르는 경향이 있더라도 !]
> dlf <- read.delim("data/DownloadFestival(No Outlier).dat", header=TRUE) # DataFrame 불러오기
> hist.day1 <- ggplot(dlf, aes(day1)) + theme(legend.position = "none") + geom_histogram(aes(y=..density..), colour="black", fill="white") + labs(x="Hygiene score on day 1", y = "Density")
> hist.day1 + stat_function(fun = dnorm, args = list(mean = mean(dlf$day1, na.rm = TRUE), sd = sd(dlf$day1, na.rm = TRUE)), colour = "black", size = 1)
# hist.day2, hist.day3 도 그리기
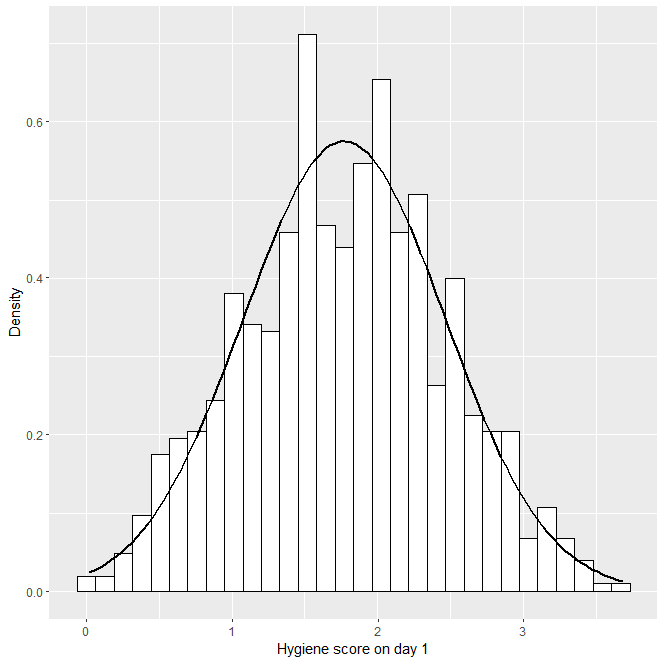
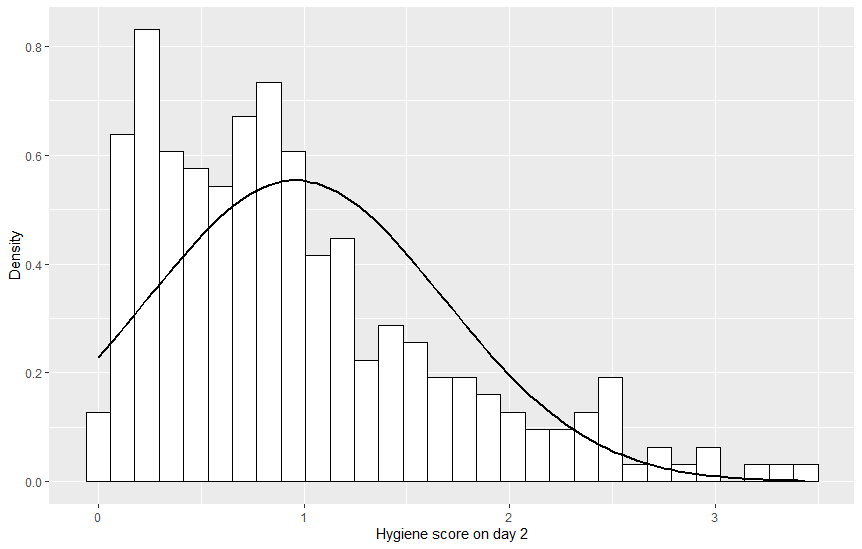
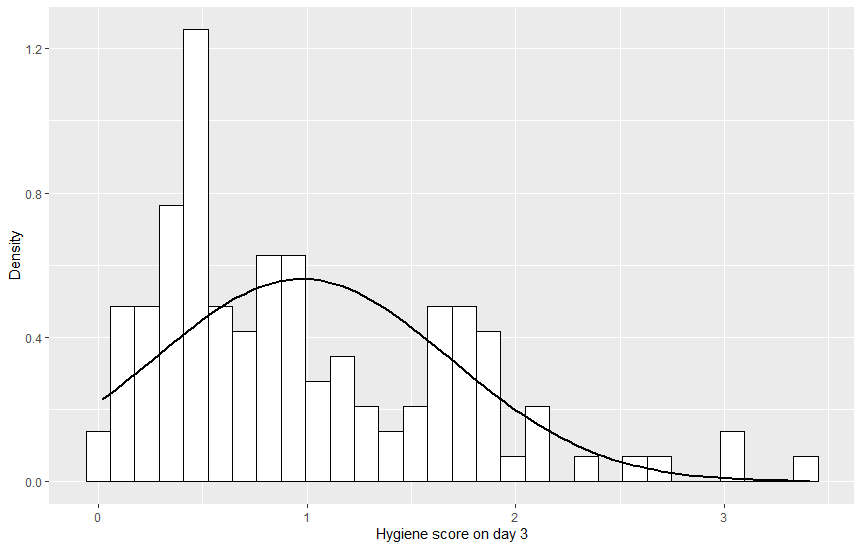
ggplot(dlf, aes(day1)) : dlf 데이터프레임에 있는 day1 변수를 그리기
geom_histogram(aes(y=..density..), colour=”black”, fill=”white”) : 선을 검은색으로 막대 내부를 흰색으로
stat_function(fun = dnorm : 정규 곡선을 그리기
mean = mean(dlf$day1, na.rm = TRUE) : 정규분포의 평균을 결측값을 모두 제거한 후의 day1 변수의 평균으로 설정
sd = sd(dlf$day1, na.rm = TRUE) : 정규분포의 표준편차를 day1 변수의 표준편차로 설정
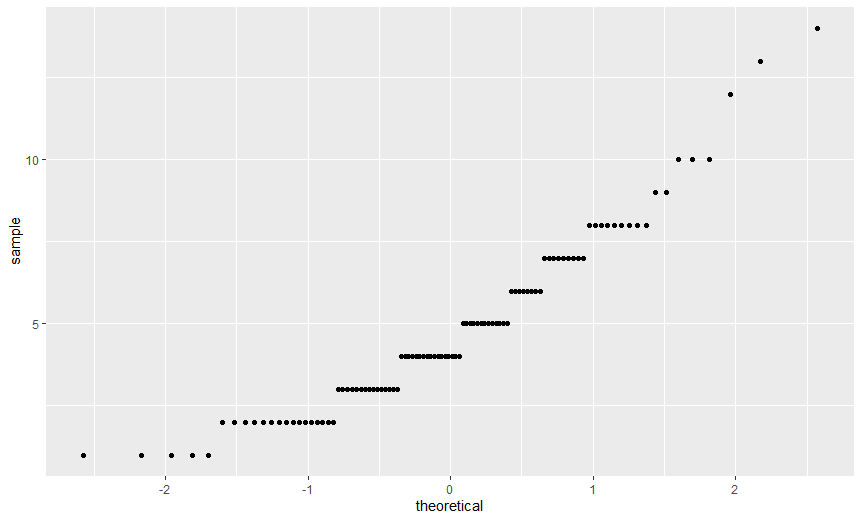
> ggplot(dlf, aes(sample=day1)) + stat_qq()
> ggplot(dlf, aes(sample=day2)) + stat_qq()
> ggplot(dlf, aes(sample=day3)) + stat_qq()
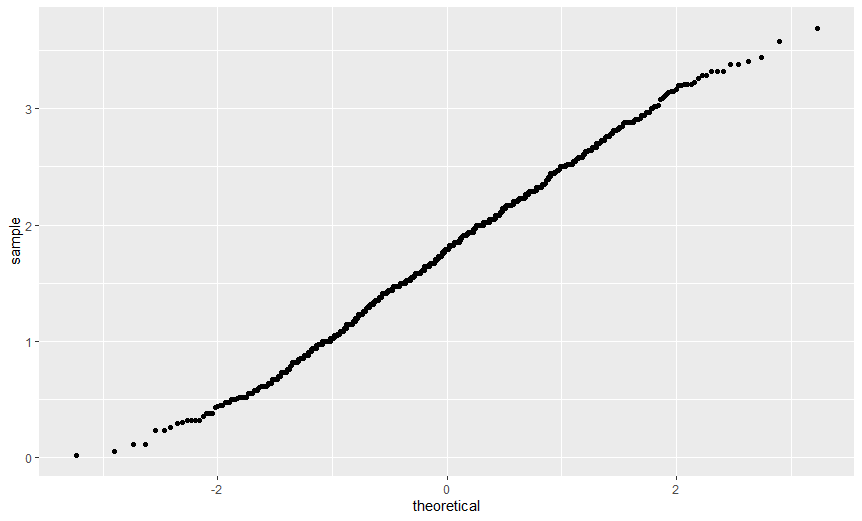
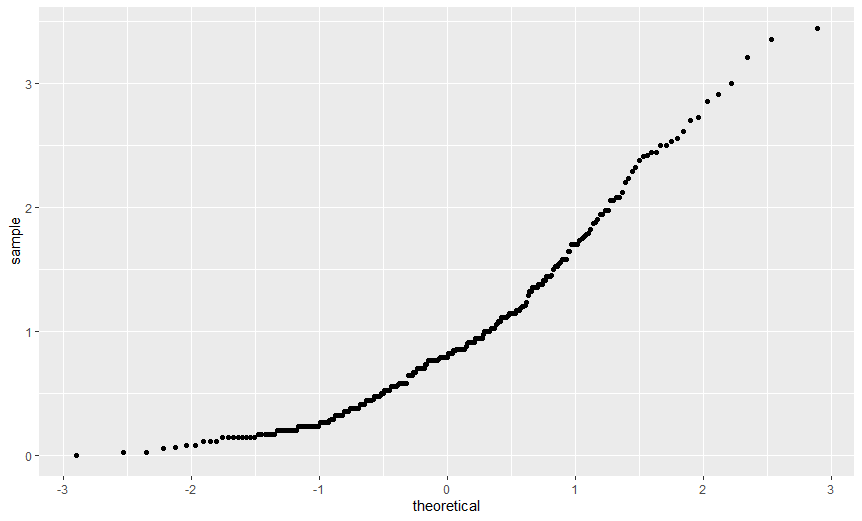
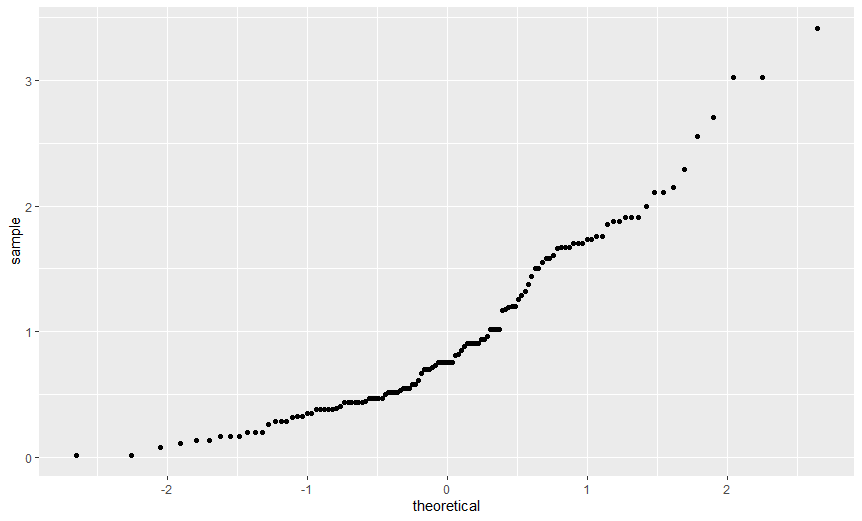
변수 day1 이 가장 정규분포에 가깝다고 생각할 수 있다.
> describe(dlf$day1)
> describe(dlf[, c("day1", "day2", "day3")]) # 묶어서 한번에 보기
# basic = FALSE : 기초 통계량 제외, norm = TRUE : 점수들의 분포에 관련된 통계량들을 표시
> stat.desc(dlf[, c("day1", "day2", "day3")], basic = FALSE, norm = TRUE) # 묶어서 한번에 보기
> round(stat.desc(dlf[, c("day1", "day2", "day3")], basic = FALSE, norm = TRUE), digits = 3) # 소수점 3째 자리까지 반올림해서 보기
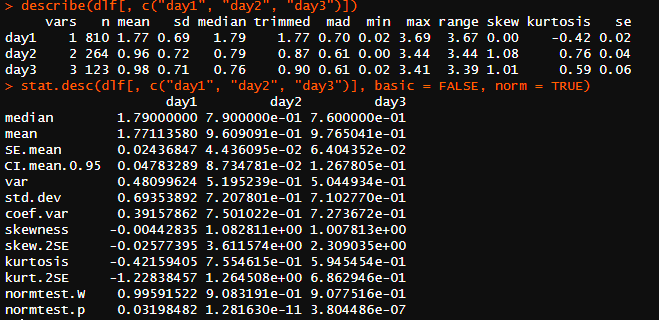
정규분포에서는 비대칭도(skewness)와 첨도(kurtosis)가 모두 0이어야 한다.
비대칭도와 첨도가 유용하긴 하지만, 이 값들을 z-score 로 변환해 보는 것도 좋다.
z-score : 실제 점수를 평균이 0, 표준편차가 1인 분포에 맞추어 변환한 값z-score 로 변환하는 값이 유용한 이유 1. 서로 다른 측정 방법으로 얻은 서로 다른 표본들의 비대칭도와 첨도를 비교할 수 있다는 점 2. 자료의 비대칭도와 첨도가 발생할 확률을 파악할 수 있다는 점| \(z_{비대칭도} = \frac{S - 평균}{SE_{비대칭도}}\) | \(z_{첨도} = \frac{K - 평균}{SE_{첨도}}\) |
절댓값이 1.96보다 큰 z-score는 p < 0.05 에서 유의 [크기가 작은 표본]
절댓값이 2.58보다 큰 z-score는 p < 0.01 에서 유의 [큰 표본]
절댓값이 3.29보다 큰 z-score는 p < 0.001 에서 유의 [아주 큰 표본]
z > 1.96 -> \(\frac{k}{1.96 * SE} > 1\) [p < 0.05, 단! 크기가 작은 표본에서 유의!]
EX. skew.2SE : -0.025 3.61 2.30 -> day2, day3의 분포가 유의하게 기울었음을 의미
> rexam <- read.delim("data/RExam.dat", header = TRUE)
> rexam$uni<-factor(rexam$uni, levels = c(0:1), labels = c("Duncetown University", "Sussex University"))
rexam 데이터프레임에 uni 컬럼의 값 0, 1 을 “Duncetown University”, “Sussex University” 로 대체
> by(data=rexam$exam, INDICES=rexam$uni, FUN=describe) # data : 분석할 자료, INDICES : 그룹화 변수, FUN : 자료에 적용할 함수
> by(rexam[, c("exam", "numeracy")], rexam$uni, stat.desc, basic = FALSE, norm = TRUE)
표본의 점수들을 그 표본과 표준편차가 같은 정규분포에서 뽑은 점수들과 비교
이 검정에서 유의하지 않은 결과(p > 0.05)가 나왔다면, 표본 분포가 정규분포와 그리 다르지 않다는 것
이 검정에서 유의한 결과가 나왔다고 해서, 이 자료의 분포는 정규분포에서 많이 벗어나니 정규성을 가정한 통계적 절차들을 사용하면 안된다고 성급하게 판단하면 안 된다.
이유 : 표본이 크면 정규분포를 조금만 벗어나도 유의한 결과가 나오기 쉽다는 점을 고려
따라서 검정에만 의존하지 말고 그래프를 그려서 눈으로도 확인해야 한다.
> shapiro.test(rexam$exam) # W = 0.96131, p-value = 0.004991 < 0.05 -> 변수가 정규성에서 이탈
> shapiro.test(rexam$numeracy) # W = 0.92439, p-value = 2.424e-05
개별 분포가 아닌 각 그룹의 분포가 중요하다!!
> by(rexam$exam, rexam$uni, shapiro.test) # 대학별로 검정 실행
# Duncetown University : W = 0.97217, p-value = 0.2829
# Sussex University : W = 0.98371, p-value = 0.7151
# 두 대학 모두 정규분포에 가깝다
> by(rexam$numeracy, rexam$uni, shapiro.test)
# Duncetown University : W = 0.94082, p-value = 0.01452
# Sussex University : W = 0.93235, p-value = 0.006787
# 두 대학 모두 유의한 수준으로 정규분포가 아니라는 결과가 나왔다.
# 그래프로 비교
> ggplot(rexam, aes(sample=exam)) + stat_qq()
> ggplot(rexam, aes(sample=numeracy)) + stat_qq()
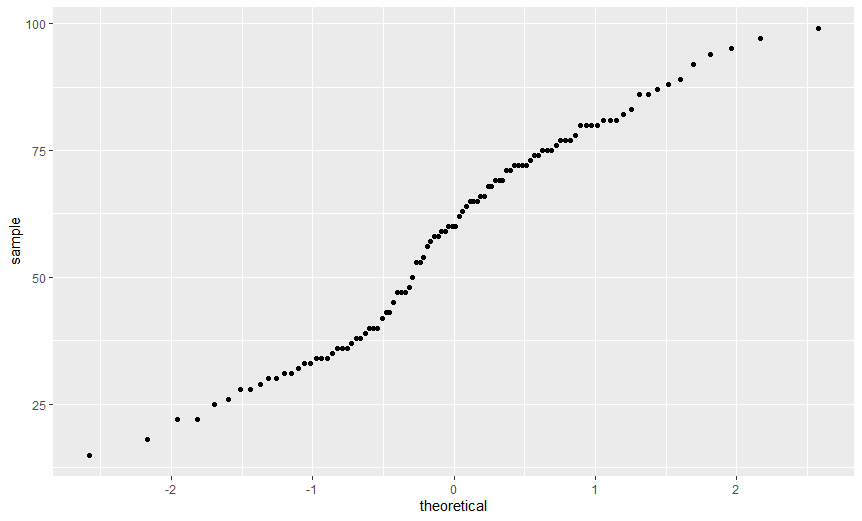
분산의 동질성 : 여러 그룹의 자료를 수집한 경우, 이 가정은 각 그룹에서 결과변수(들)의 분산이 동일해야 한다는 뜻
서로 다른 그룹의 분산이 같을 것이라는 귀무가설을 검정
만일 레빈 검정이 p <= 0.05 에서 유의하다면 귀무가설은 거짓이며, 따라서 분산들이 유의하게 다르다는 뜻
이런 경우 분산들의 동질성 가정이 성립하지 않는다.
> leveneTest(rexam$exam, rexam$uni, center = median) # F(1, 98) = 2.09, p=0.15 이므로 대학생들의 분산은 그리 다르지 않다.
> leveneTest(rexam$numeracy, rexam$uni, center = median) # F(1, 98) = 5.37, p=0.02 이므로 분산들이 유의하게 다르며, 분산의 동질성 가정이 깨졌다.
Discovering Statistics Using R - 010 [ 2024년12월25일 ]
Discovering Statistics Using R - 009 [ 2024년12월12일 ]
Discovering Statistics Using R - 008 [ 2024년12월10일 ]
Discovering Statistics Using R - 007 [ 2024년12월06일 ]
Discovering Statistics Using R - 006 [ 2024년12월05일 ]
Discovering Statistics Using R - 005 [ 2024년12월04일 ]
Discovering Statistics Using R - 004 [ 2024년12월03일 ]
Discovering Statistics Using R - 003 [ 2024년11월30일 ]