

regression analisys : 하나의 모형을 자료에 적합시키고 그것을 이용해서 하나 이상의 독립변수들로부터 종속변수의 값들을 예측하는 것
잔차 : 선(=모형)과 실제 자료의 수직 거리
모형이 자료에서 벗어난 정도 = \(\sum(관측값 - 모형)^2\) = \(총제곱합(= SS_T)\) = \(잔차제곱합(=SS_R)\)
\(SS_M\) : Y의 평균값과 회귀선의 차이들로 이루어진다.
\(R^2 = \frac{SS_M}{SS_T}\)
회귀분석인 경우 자유도는 N-P-1 [ N : 표본 크기, P : 예측변수의 개수]
# lm(결과변수 ~ 예측변수(들), data = dataFrame, na.action = 결측값 처리 방식)
> albumSales.1 <- lm(sales ~ adverts, data = album1)
> summary(albumSales.1)
Call:
lm(formula = sales ~ adverts, data = album1)
Residuals:
Min 1Q Median 3Q Max
-152.949 -43.796 -0.393 37.040 211.866
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.341e+02 7.537e+00 17.799 <2e-16 ***
adverts 9.612e-02 9.632e-03 9.979 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 65.99 on 198 degrees of freedom
Multiple R-squared: 0.3346, Adjusted R-squared: 0.3313
F-statistic: 99.59 on 1 and 198 DF, p-value: < 2.2e-16
# 피어슨 상관계수(R)
> sqrt(0.3346)
[1] 0.5784462
F 비는 99.59 [ 이 값은 p<0.001수준에서 유의하다 ]
이 결과는 만일 귀무가설이 참이라면 이 F비가 나올 확률이 0.1% 미만이라는 뜻
따라서, 회귀모형을 이용해서 음반 판매량을 예측하는 것이 음반 판매량의 평균을 사용해서 판매량을 예측할 때보다 유의하게 더 낫다는 결론을 내릴 수 있다.
이 관측 유의확률이 0.05보다 작으면, 그 결과가 진짜 효과를 반영한다는데 동의
따라서, 광고비가 음반 판매량 예측에 유의하게(p < 0.001) 기여한다.
\(결과_i = (모형) + 오차_i\)
\(R^2\)의 큰 문제점은 모형에 변수를 추가할수록 \(R^2\) 값이 점점 커진다는 점
이를 극복하기 위한 수단으로, 아카이케 정보기준(akaike information criterion, AIC)를 사용 : 예측변수가 많을수록 벌점을 준다는 특징이 있다.
\(AIC = nln(\frac{SSE}{n}) + 2k\) -> SSE : 모형의 오차제곱합, k는 예측변수 개수[벌점에 해당]
AIC값이 크다는 것은 모형이 덜 적합하다는 뜻
특이한 점은 AIC 값이 크다 작다를 판단할 수 있는 기준점이 없다는 점, 그리고 같은 자료에 대한 모형들만 비교할 수 있다는 점
과거 연구에 기초해서 예측변수들을 선택하되, 그 예측변수들을 모형에 도입하는 순서를 실험자가 결정
모든 예측변수를 모형에 동시에 도입하는 것
전진 : 상수(\(b_0\))만 있는 상태로 시작한 후 변수 하나씩 추가하여 AIC를 사용하여 추가할지 판단
후진 : 모든 예측변수를 모형에 추가한 후 변수를 하나씩 제거하면서 AIC가 낮아지는지 확인
단계별 방법을 사용할 때는 후진 방법이 좋다.
이는 억제인자 효과 때문인데, 예측변수가 효과를 가지되 다른 어떤 변수를 고정했을 때만 효과를 가지는 경우에 발생
전진 방향에서는 제2종 오류를 범할 위험이 크다.
단계별 방법의 문제점 : 이미 모형에 존재하는 다른 변수들에 기초해서 한 변수의 적합도를 평가
전부분집합 회귀 : 변수들의 모든 집합(부분집합)을 시도해서 최량적합을 찾는다.
단점은 예측변수의 수가 늘어남에 따라 가능한 부분집합의 수가 지수적으로 늘어난다.
IF 이상치가 존재, then 잔차가 큰 값이 존재.
-> 이러한 잔차는 비표준화잔차라고 하는데 이 문제를 극복하기 위해 표준화잔차를 사용
-> 표준화잔차 = 보통의 잔차 / 표준편차 추정값
이런 사례가 있다면, 삭제했을 때 회귀계수들이 달라지는지를 확인해야 한다.
만일 해당 사례가 사실은 모형에 그리 큰 영향을 미치지 않았다면 수정 예측값은 원래의 예측값과 아주 비슷할 것
DFFit : 수정 예측값과 원래의 예측값의 차이
평균 지렛대 값 = \((k+1) / n\) [ k : 모형의 예측변수 개수, n : 참가자의 수 ]
지렛대 값은 0(사례가 예측에 아무런 영향을 주지 않음) ~ 1(사례가 예측에 완전한 영향을 줌)까지
- 중요한 한마디
만일 어떤 점이 Y 축에서 유의한 이상치로 판명되었지만 그 점의 쿡의 거리가 < 1 이면, 그 점은 회귀분석에 큰 영향을 미치지 않으므로 굳이 삭제할 필요가 없다.
그러나, 모형이 그런 점에 적합되지 않은 이유를 이해하기 위해 그런 점을 좀 더 연구할 필요는 있다.
모든 예측변수는 양적 변수 또는 범주형 변수 이어야 한다.
결과변수는 반드시 연속이자 비유계(unbounded)인 양적 변수이어야 한다.
결과를 모형만큼이나 잘 예측할 수 있는 다른 변수들이 존재하는 것이므로
이를 자기상관(autocorrelation)이 없다고 말한다.
오차들의 이연상관을 검사하는 더빈-왓슨 검정으로 확인할 수 있다.
\(R^2\) 값이 표본에서 얻은 회귀모형이 Y의 변동을 얼마나 설명하는지 말해주는 값
수정 \(R^2\) 값은 만일 표본이 얻은 모집단으로부터 회귀모형을 유도했다면 그 모형이 Y의 변동을 얼마나 설명할 것인지를 말해주는 값
R은 훼리 방정식을 통해 수정된 \(R^2\) 값을 계산해주는데 이 공식은 회귀모형이 완전히 다른 자료 집합을 얼마나 잘 예측할 것인지에 관해서는 아무것도 말해주지 않는다.
따라서 스타인의 공식을 사용한다. -> \(수정 R^2 = 1 - [(\frac{n-1}{n-k-1})(\frac{n-2}{n-k-2})(\frac{n+1}{n})](1-R^2)\) | n : 참가자의 수, k : 모형의 예측변수의 개수
둘 다 관심이 있다면 큰 값을 사용하면 OK
만약 하나의 예측변수가 다른 어떤 예측변수와 완벽한 선형관계일 때 완전공선성이 존재한다고 말한다.
해결법 : 분산팽창인자(variance inflation factor, VIF) : 주어진 한 예측변수가 다른 예측변수(들)와 강한 선형 관계를 가지고 있는지를 말한다.
VIF값이 10 이상이라면 걱정할 필요가 있다고 제시
또한, 만일 평균 VIF값이 1보다 크면 다중공선성 때문에 회귀모형이 편향될 수 있다.
> albumSales.2<-lm(sales ~ adverts, data = album2)
> albumSales.3<-lm(sales ~ adverts + airplay + attract, data = album2) # 다중 회귀
> summary(albumSales.2)
Call:
lm(formula = sales ~ adverts, data = album2)
Residuals:
Min 1Q Median 3Q Max
-152.949 -43.796 -0.393 37.040 211.866
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.341e+02 7.537e+00 17.799 <2e-16 ***
adverts 9.612e-02 9.632e-03 9.979 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 65.99 on 198 degrees of freedom
Multiple R-squared: 0.3346, Adjusted R-squared: 0.3313
F-statistic: 99.59 on 1 and 198 DF, p-value: < 2.2e-16
R = 0.3346 : 광고비가 음반 판매량 변동의 33.5%를 설명
\(R^2 = 0.5784\)
> summary(albumSales.3)
Call:
lm(formula = sales ~ adverts + airplay + attract, data = album2)
Residuals:
Min 1Q Median 3Q Max
-121.324 -28.336 -0.451 28.967 144.132
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -26.612958 17.350001 -1.534 0.127
adverts 0.084885 0.006923 12.261 < 2e-16 ***
airplay 3.367425 0.277771 12.123 < 2e-16 ***
attract 11.086335 2.437849 4.548 9.49e-06 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 47.09 on 196 degrees of freedom
Multiple R-squared: 0.6647, Adjusted R-squared: 0.6595
F-statistic: 129.5 on 3 and 196 DF, p-value: < 2.2e-16
R = 0.6647 : 예측변수들이 음반 판매량 변동의 66.5%를 설명
따라서 방송 횟수와 매력은 또 다른 33%(= 66.5% - 33.5%)에 해당
판매량 = -26.61 + (0.08 * 광고비) + (3.38 * 방송홧수) + (11.09 * 매력)
Pr(>|t|) < 0.05 보다 작으면 해당 예측변수는 모형에 유의한 수준으로 기여한다고 할 수 있다. 그리고 t값이 클수록 예측변수의 기여도가 커진다.
> lm.beta(albumSales.3) # 표준화된 벡터를 구하는 공식
adverts airplay attract
0.5108462 0.5119881 0.1916834
이 추정값들은 예측변수의 표준편차가 1 단위 변할 때의 결과변수의 표준편차의 변화량이다.
> confint(albumSales.3) # 각 추정값의 신뢰구간을 구하는 함수
2.5 % 97.5 %
(Intercept) -60.82960967 7.60369295
adverts 0.07123166 0.09853799
airplay 2.81962186 3.91522848
attract 6.27855218 15.89411823 # 조금 넓긴 한데 0을 포함하지 않고 있으며 다른 변수들보다 이 변수의 매개변수 추정값이 참값을 덜 대표한다.
좋은 모형의 신뢰구간은 그 범위가 좁다.
b의 부호(양, 음)는 예측변수와 결과변수의 관계의 방향을 말해준다.
따라서 아주 나쁜 모형의 신뢰구간은 0을 포함할 것이다.
둘째 모형의 \(R^2\)이 첫 모형의 \(R^2\)보다 유의하게 더 큰지 판단해야 한다.
\(R^2\)의 유의성은 F비로 검사할 수 있다.
\(F = \frac{(N-k-1)R^2}{k(1-R^2)}\)
> anova(albumSales.2, albumSales.3)
Analysis of Variance Table
Model 1: sales ~ adverts
Model 2: sales ~ adverts + airplay + attract
Res.Df RSS Df Sum of Sq F Pr(>F)
1 198 862264
2 196 434575 2 427690 96.447 < 2.2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
F 값 = 96.447, Pr(>F) = 2.2e-16 < 0.001 이므로 albumSales.2에 비해 albumSales.3가 자료에 유의한 수준으로 더 적합
> album2$residuals<-resid(albumSales.3) # 잔차
> album2$standardized.residuals <- rstandard(albumSales.3) # 표준화잔차
> album2$studentized.residuals <- rstudent(albumSales.3) # 스튜던트화 잔차
> album2$cooks.distance<-cooks.distance(albumSales.3) # 쿡의 거리
> album2$dfbeta <- dfbeta(albumSales.3) # DFBeta
> album2$dffit <- dffits(albumSales.3) # DFFit
> album2$leverage <- hatvalues(albumSales.3) # hat-value
> album2$covariance.ratios <- covratio(albumSales.3) # 공분산비
# 보통의 표본에서는 사례의 95%는 표준화잔차가 약 +-2% 이내라고 기대한다.
> album2$large.residual <- album2$standardized.residuals > 2 | album2$standardized.residuals < -2 # 각 사례에 잔차가 -2보다 작거나 +2보다 큰 값 찾기
> sum(album2$large.residual) # 12
# 공분산비에 대해서 기준 적용
# CVR_i > 1 + [3(k+1)/n] = 1 + [3(3+1)/200] = 1.06
# CVR_i < 1 - [3(k+1)/n] = 1 - [3(3+1)/200] = 0.94
> album2$out.cvr <- album2$covariance.ratios > 1.06 | album2$covariance.ratios < 0.94
> sum(album2$out.cvr) # 21
> durbinWatsonTest(albumSales.3) # == dwt(albumSales.3)
lag Autocorrelation D-W Statistic p-value
1 0.0026951 1.949819 0.722
Alternative hypothesis: rho != 0
검정 통계량이 1보다 작거나 3보다 크면 주의할 필요가 있다는 것[이 값은 2에 가까울수록 좋다, 여기서는 1.95]
여기서 p > 0.05 이므로, 이 검정통계량은 전혀 유의하지 않다.
> vif(albumSales.3)
adverts airplay attract
1.014593 1.042504 1.038455
> 1/vif(albumSales.3)
adverts airplay attract
0.9856172 0.9592287 0.9629695
> mean(vif(albumSales.3))
[1] 1.03185
결론 : 우리의 모형에 다중공선성이 존재하지는 않는다고 결론을 내려도 안전
> plot(albumSales.3)
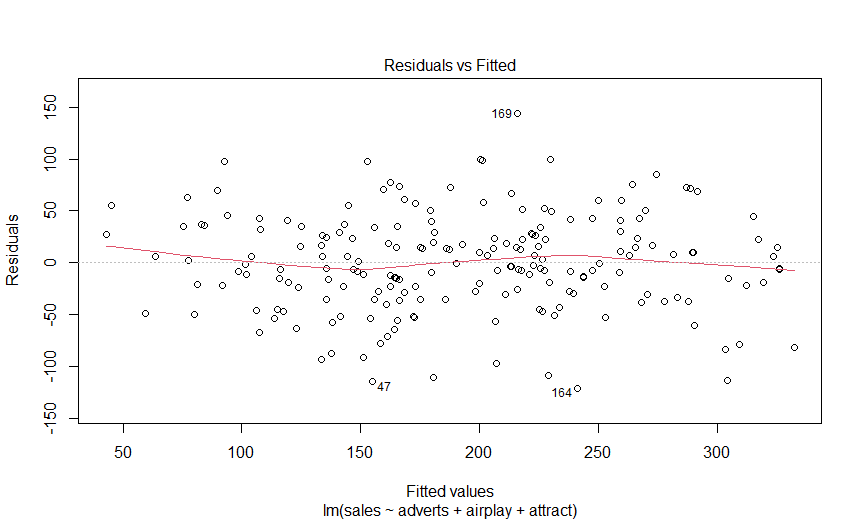
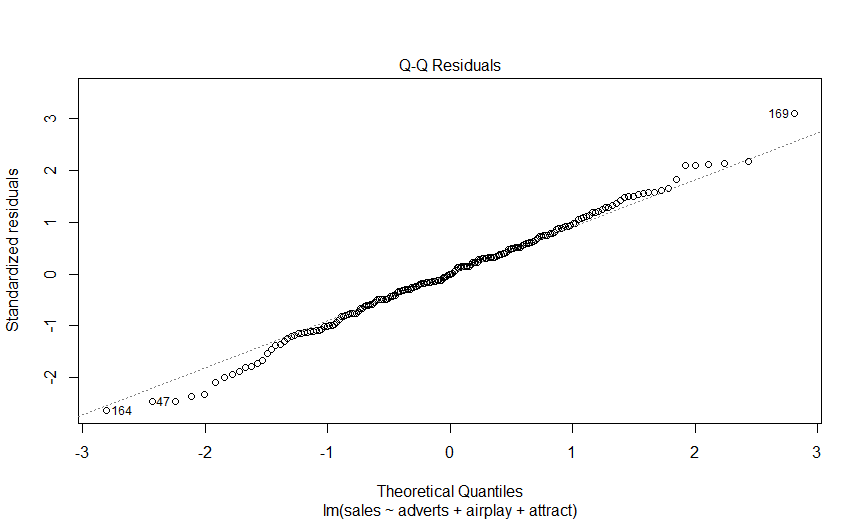
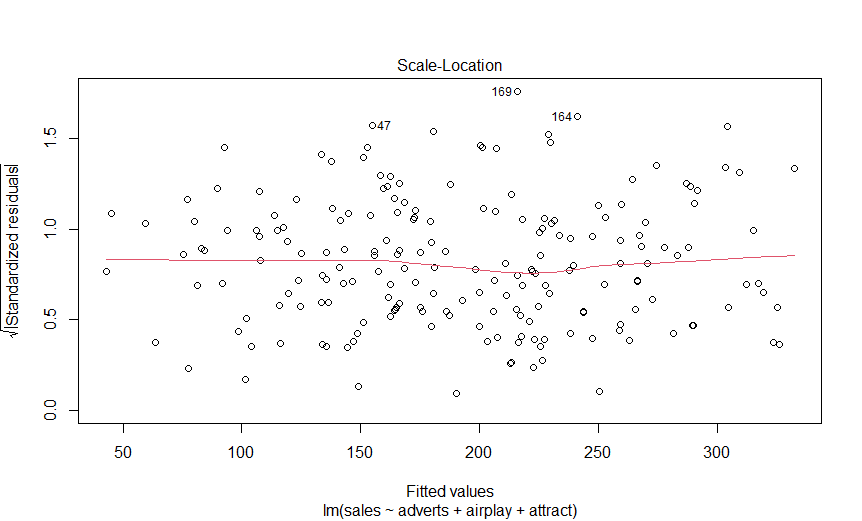
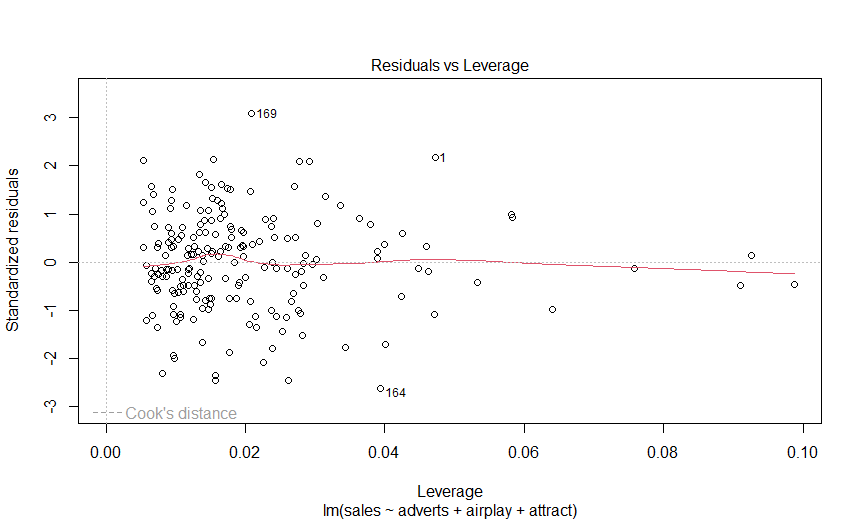
> bootReg<-function(formula, data, i)
+ {
+ d <- data[i,]
+ fit <- lm(formula, data = d)
+ return(coef(fit)) # 주어진 모형의 절편과 예측변수들의 기울기 계수들을 출력
+ }
> bootResults<-boot(statistic = bootReg, formula = sales ~ adverts + airplay + attract, data = album2, R = 2000) # 부트스트랩 표본 얻기
> boot.ci(bootResults, type = "bca", index = 1) # bca : 신뢰구간의 종류, index : 통계량의 위치(1 = 절편)
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 2000 bootstrap replicates
CALL :
boot.ci(boot.out = bootResults, type = "bca", index = 1)
Intervals :
Level BCa
95% (-55.26, 9.02 )
Calculations and Intervals on Original Scale
절편의 신뢰구간 : -55.26 ~ 9.02
이러한 신뢰구간은 앞에서 대입(plug-in) 접근방식으로 얻은 신뢰구간과 비교해보자(여기서는 상당히 비슷하다)
| — | \(R^2\) | B | SE B | \(\beta\) | p |
| 단계 1 | 0.34 | — | — | — | <.001 |
| 상수 | — | 134.14 | 7.54 | — | <.001 |
| 광고비 | — | 0.10 | 0.01 | 0.58* | <.001 |
| 단계 2 | 0.33 | — | — | — | <.001 |
| 상수 | — | -26.61 | 17.35 | — | .127 |
| 광고비 | — | 0.09 | 0.01 | 0.51* | <.001 |
| BBC 라디오 1 방송 횟수 | — | 3.37 | 0.28 | 0.51* | <.001 |
| 밴드 매력 | — | 11.09 | 2.44 | 0.19* | <.001 |
범주형 변수를 예측변수로 사용하려고 할 때 문제는, 사용하려는 범주형 변수의 범주의 개수가 두 개를 넘는다.
Ex. 종교 : 이슬람교, 유대교, 가톨릭, …
해결책 -> 가변수(dummy variable)사용 [ 부호화하고자 하는 그룹(집단)의 개수에서 1을 뺀 것만큼 변수를 생성]
> head(gfr, n = 10)
ticknumb music day1 day2 day3 change
1 2111 Metaller 2.65 1.35 1.61 -1.04
2 2229 Crusty 0.97 1.41 0.29 -0.68
3 2338 No Musical Affiliation 0.84 NA NA NA
4 2384 Crusty 3.03 NA NA NA
5 2401 No Musical Affiliation 0.88 0.08 NA NA
6 2405 Crusty 0.85 NA NA NA
7 2467 Indie Kid 1.56 NA NA NA
8 2478 Indie Kid 3.02 NA NA NA
9 2490 Crusty 2.29 NA NA NA
10 2504 No Musical Affiliation 1.11 0.44 0.55 -0.56
music 컬럼이 문자열
> gfr$music <- factor(gfr$msuic) # 요인으로 변경
> contrasts(gfr$music)<-contr.treatment(4, base = 4)
# contrasts(gfr$music) : gfr 데이터프레임의 변수 music 에 대한 대비를 설정
# contr.treatment(그룹 수, base = 기저 그룹의 번호) : 모든 그룹을 하나의 기저 조건과 비교한 결과에 기초해서 대비를 계산
> gfr$music
attr(,"contrasts")
1 2 3
Crusty 1 0 0
Indie Kid 0 1 0
Metaller 0 0 1
No Musical Affiliation 0 0 0
Levels: Crusty Indie Kid Metaller No Musical Affiliation
# 위 과정에 변수 이름 설정하는 방법
> crusty_v_NMA<-c(1, 0, 0, 0)
> indie_v_NMA<-c(0, 1, 0, 0)
> metal_v_NMA<-c(0, 0, 1, 0)
> contrasts(gfr$music)<-cbind(crusty_v_NMA, indie_v_NMA, metal_v_NMA)
attr(,"contrasts")
crusty_v_NMA indie_v_NMA metal_v_NMA
Crusty 1 0 0
Indie Kid 0 1 0
Metaller 0 0 1
No Musical Affiliation 0 0 0
Levels: Crusty Indie Kid Metaller No Musical Affiliation
> glastonburyModel<-lm(change ~ music, data = gfr)
> summary(glastonburyModel)
Call:
lm(formula = change ~ music, data = gfr)
Residuals:
Min 1Q Median 3Q Max
-1.82569 -0.50489 0.05593 0.42430 1.59431
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.55431 0.09036 -6.134 1.15e-08 ***
musiccrusty_v_NMA -0.41152 0.16703 -2.464 0.0152 *
musicindie_v_NMA -0.40998 0.20492 -2.001 0.0477 *
musicmetal_v_NMA 0.02838 0.16033 0.177 0.8598
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.6882 on 119 degrees of freedom
(결측으로 인하여 687개의 관측치가 삭제되었습니다.)
Multiple R-squared: 0.07617, Adjusted R-squared: 0.05288
F-statistic: 3.27 on 3 and 119 DF, p-value: 0.02369
\(R^2\) = 7.6% -> 위생 점수 변화량의 변동의 7.6%는 참가자의 음악 취향으로 설명된다.
F 통계량에 따르면, 이 모형은 모형이 없을 때보다 위생 점수의 변화를 유의한 수준으로 더 잘 예측한다.
> round(tapply(gfr$change, gfr$music, mean, na.rm=TRUE), 3)
Crusty Indie Kid Metaller No Musical Affiliation
-0.966 -0.964 -0.526 -0.554
크러스티 그룹과 무취향 그룹 평균의 차이는 -0.966 - (-0.554) = -0.412 이다.
따라서, 크러스티 그룹의 위생 점수 변화가 무취향 그룹의 위생 점수 변화보다 크다.
Discovering Statistics Using R - 010 [ 2024년12월25일 ]
Discovering Statistics Using R - 009 [ 2024년12월12일 ]
Discovering Statistics Using R - 008 [ 2024년12월10일 ]
Discovering Statistics Using R - 007 [ 2024년12월06일 ]
Discovering Statistics Using R - 006 [ 2024년12월05일 ]
Discovering Statistics Using R - 005 [ 2024년12월04일 ]
Discovering Statistics Using R - 004 [ 2024년12월03일 ]
Discovering Statistics Using R - 003 [ 2024년11월30일 ]